Cliodynamics and Mathematical Models in History. Part 1

What is Cliodynamics?

‍Peter Turchin's pioneering work in cliodynamics uses mathematical modeling to investigate deterministic patterns in historical processes, balancing social predictability with inherent randomness.

The term “cliodynamics” was proposed in 2003 by Peter Turchin, an American physicist of Russian descent. Such refers to an interdisciplinary field of research on long-term historical processes, which are based upon the development of diverse mathematical models whilst employing differential equations as a tool. As a basis for construction, Turchin formed models on the notion of “asabiyyah”, which was established in the XIV century by the Arab philosopher Ibn Khaldun. Ibn Khaldun considered the term "asabiyyah" to mean the degree of social solidarity in a community and the extent to which that society is capable of collective action to preserve its state and itself.

Immanuel Kant once wrote – “In any special doctrine of nature there can be only as much proper science as there is mathematics therein”. Mathematical calculations, however, entail rigorous determinism, in other words, the result of which is always predetermined, hence, rising important questions. Do historical processes have the properties of determinism? Is it feasible to employ mathematical instruments to formalise these processes?

To what extent will the components of high stochasticity (randomness) of historical processes impact the final results of a calculation? Peter Turchin chose to investigate the issue by employing medieval agrarian societies as an example, presuming their mathematical framework is far less complex than it would be if they were modelling the historical dynamics of later, industrial states of the New Age. Turchin rightly noted that more than 95% of written history is the history of agrarian societies. That is to say, as per time and geographical framework for research, he chose the history of Europe in the period 500-1800.

During the development of modelling approaches, Turchin opted to focus on the usage of multi-agent modelling, which is distinguished by the presence of the properties of autonomy, limited representation, and decentralisation. Autonomy denotes agents' total or partial independence; limited representation indicates agents' lack of comprehensive awareness of the system due to its complexity. Finally, decentralisation implies that none of the agents have the ability to manage the entire system as a whole. As previously stated, the modelling language was based on differential equations.

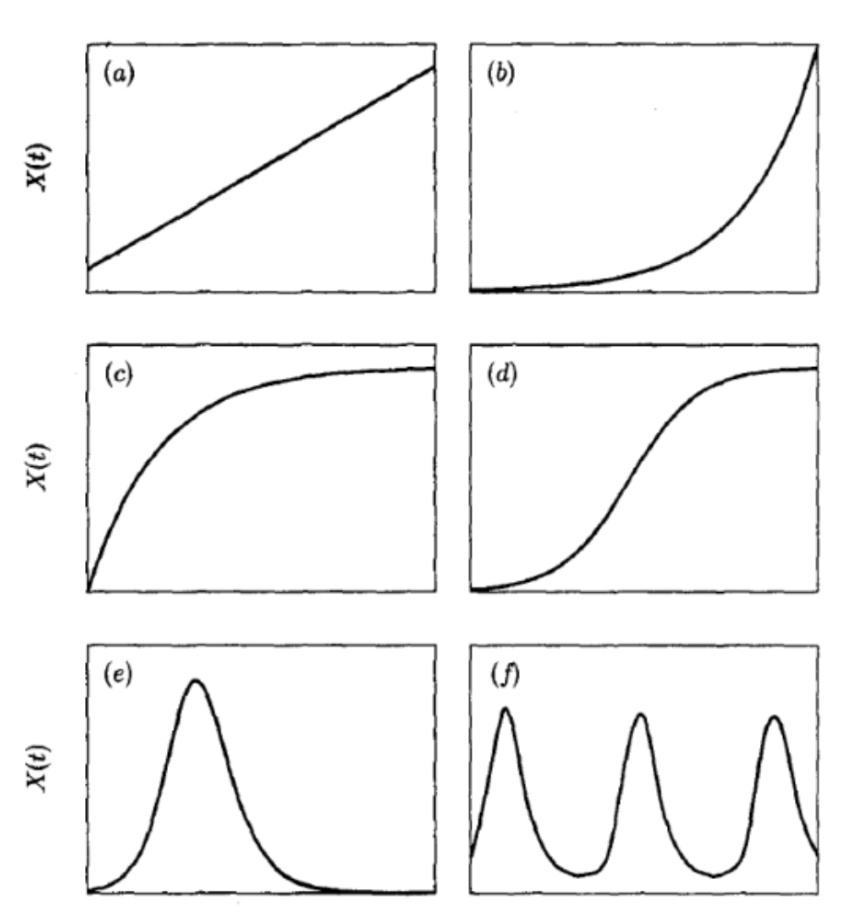
Turchin explored various forms of dynamic processes of state expansion for the mathematical study of geopolitical models, among which he defined the following patterns of growth: linear (limitless) (a), exponential (b), asymptotic (c), logistic (d), "rise and fall" (e), as well as undamped fluctuations (f). As per rightful belief, that the nature of the dynamics of the natural historical process cannot be of unlimited or exponential type of growth, due to limited resources as well as the constant influence of some states on others, he came to the conclusion that it is inevitable to introduce a negative feedback component into the models. This, in turn, leads to models that assume either an asymptotic equilibrium of growth or oscillatory conceptions of "rise and fall".

‍

‍

Read the second part following this link.