Cliodynamics and Mathematical Models in History. Part 3
Practical visualisation
(Continued. See Part 1, Part 2)
Artzrouni and Komlos's spatial model provides a computational lens to study territorial evolution in Europe, prompting Peter Turchin to explore additional dynamics like Ibn Khaldun's "asabiyyah" for a more nuanced understanding of empire rise and fall.
To move on to the practical visualisation of the mathematical model of geopolitics in historical dynamics, let us consider the spatial model of territorial dynamics proposed by Artzrouni and Komlos in 1996. The researchers presented the map of Europe as a grid of square territories with linear dimensions of approximately 40 by 40 kilometres. At the initial time point (500 AD), a simulated space was created, filled with states of equal sizes (5 by 5 squares). That is, each initial "state" occupied an area of around 40,000 square kilometres on the map.
The Artzrouni and Komlos model assumed that each state's military power function had the following mathematical form:
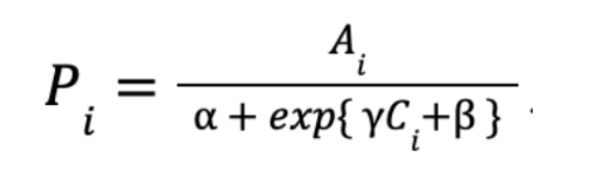
Where A and C are the area and the perimeter of the state, and α, β, γ are positive constants. In this model, the negative correlation with the "Rear Load" parameter outweighs the positive correlation from increased territory, causing the magnitude of the state's power to eventually decline to zero.
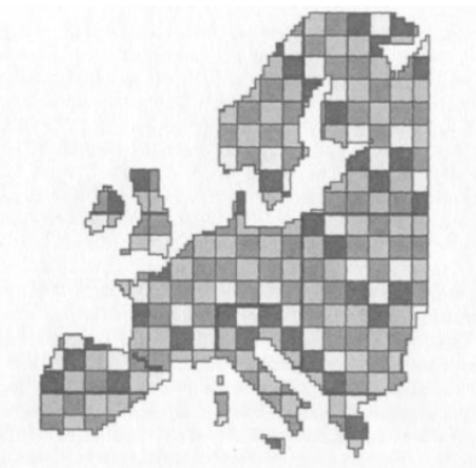
After the mathematical model ran all iterations from the year 500 to 1800, the following map was obtained as a result:

The map clearly illustrates the borders of such states as Spain, France, the United Kingdom, Sweden, Greece, and Poland (in our historical reality, as of 1800, not existing). In southern Italy, the features of the Kingdom of Naples begin to emerge. The German and Austrian states were found to be slightly "trimmed down," while there are a number of states on the map that did not exist at the period in real history. In fact, this model confirms that coastal countries are formed with a greater degree of historical certainty than inland countries, where the stochastic component has the greatest influence on the result. When simulating a dynamic process, one of the countries was chosen at random, and its strength was compared with the strength of all its neighbours. The countries with the greatest power disparity began a war, which the militarily powerful country won, with some probability indicated by the formula:
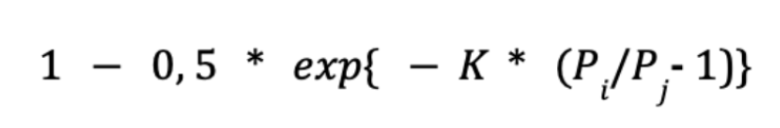
Where Pi and Pj are the power of the warring countries, and K is an additional coefficient. Each iteration corresponded to a period of four months. In point of fact, the researchers were faced with the task of how to correctly select all the parameters for the equations in order to get a picture close to historical reality. The model's evident flaw is that the indicator of the country's peripherality takes precedence over the other elements of the geopolitical model and shows a visible influence of the state's favourable border position. Nevertheless, this model confirms the fact that large countries continue to expand until the “burden of empire” compels them to stabilise their size.
Returning to Collins' geopolitical theory, it follows that, in the end, every empire should always expect the process of annihilation, because the major mechanism of decline is the delay in reaction time to changes in other model variables. Research into the rise/fall of various states by the political scientist Rein Taagepera has revealed quite frequent cases of long periods of decline of large empires. This occurs as a result of the so-called "second-order dynamics," in which the correlation between the parameters of the models operates with some delay. Turchin concludes that models based solely on geopolitical mechanisms are incapable of predicting the exact dynamics of empire growth or collapse, and that other mechanisms for empire growth or collapse should be sought, one of which may be the very "asabiyyah" of Ibn Khaldun, or in other words, the collective solidarity of communities capable of self-organization and protection.
To be continued.






.jpg)